在准备机试的时候(2025年03月14日),遇到这道题，第一次没想出来解答，于是查看了官方的解法。本人想举一反三，将代码进行修改，却发现了原解没遇见的边界问题。，现分析为什么原代码可以，现在的代码不行

原题

题目链接

已知一个长度为 n 的数组，预先按照升序排列，经由 1 到 n 次 旋转 后，得到输入数组。例如，原数组 nums = [0,1,2,4,5,6,7] 在变化后可能得到：

  • 若旋转 4 次，则可以得到 [4,5,6,7,0,1,2]
  • 若旋转 7 次，则可以得到 [0,1,2,4,5,6,7]

注意，数组 [a[0], a[1], a[2], ..., a[n-1]] 旋转一次 的结果为数组 [a[n-1], a[0], a[1], a[2], ..., a[n-2]] 。

给你一个元素值 互不相同 的数组 nums ，它原来是一个升序排列的数组，并按上述情形进行了多次旋转。请你找出并返回数组中的 最小元素 。

你必须设计一个时间复杂度为 O(log n) 的算法解决此问题。

思路

本体的思路我学习的官方题解，思路也搬运过来

方法：二分查找

思路与算法

一个不包含重复元素的升序数组在经过旋转之后，可以得到下面可视化的折线图：

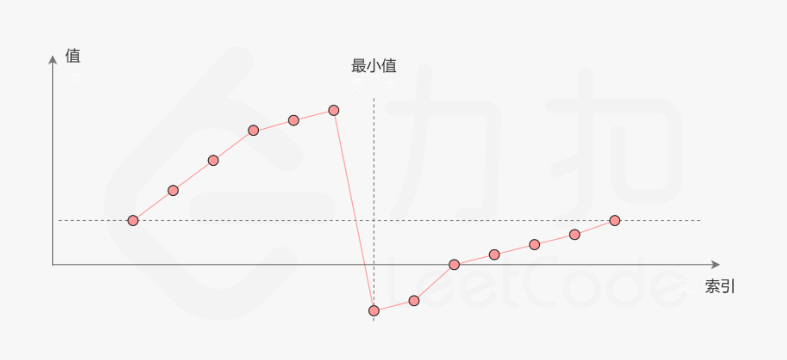
其中横轴表示数组元素的下标，纵轴表示数组元素的值。图中标出了最小值的位置，是我们需要查找的目标。

我们考虑数组中的最后一个元素 x：在最小值右侧的元素（不包括最后一个元素本身），它们的值一定都严格小于 x；而在最小值左侧的元素，它们的值一定都严格大于 x。因此，我们可以根据这一条性质，通过二分查找的方法找出最小值。

在二分查找的每一步中，左边界为 low，右边界为 high，区间的中点为 pivot，最小值就在该区间内。我们将中轴元素 nums[pivot] 与右边界元素 nums[high] 进行比较，可能会有以下的三种情况：

第一种情况是 nums[pivot]<nums[high]。如下图所示，这说明 nums[pivot] 是最小值右侧的元素，因此我们可以忽略二分查找区间的右半部分。

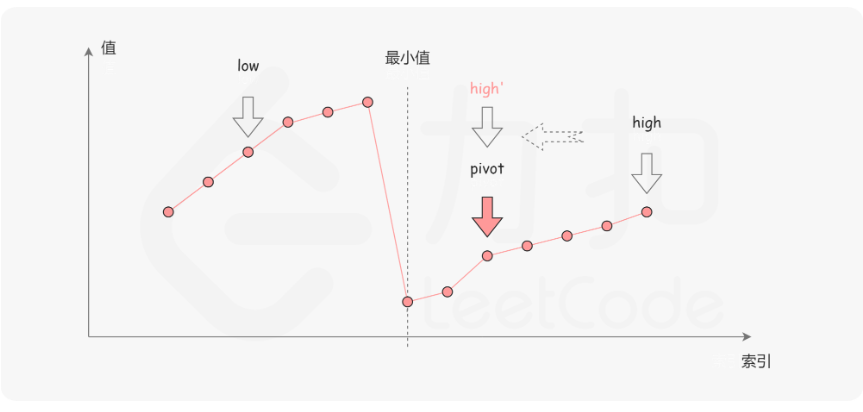
第二种情况是 nums[pivot]>nums[high]。如下图所示，这说明 nums[pivot] 是最小值左侧的元素，因此我们可以忽略二分查找区间的左半部分。

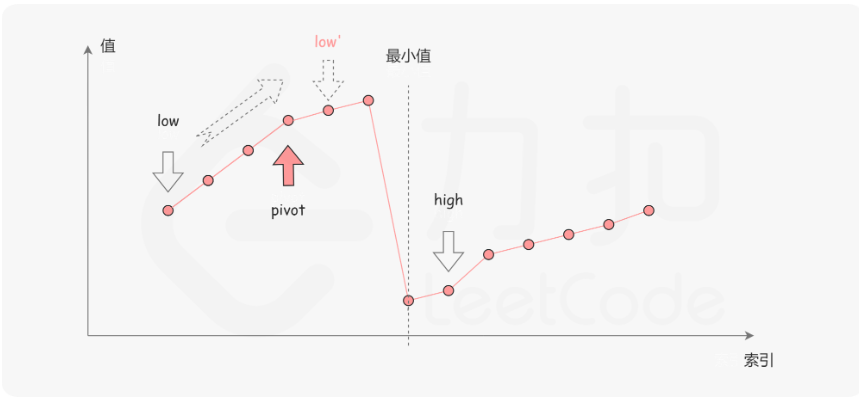
由于数组不包含重复元素，并且只要当前的区间长度不为 1，pivot 就不会与 high 重合；而如果当前的区间长度为 1，这说明我们已经可以结束二分查找了。因此不会存在 nums[pivot]=nums[high] 的情况。

当二分查找结束时，我们就得到了最小值所在的位置。

答案

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
int findMin(vector < int > & nums) {
    int left = 0;
    int right = nums.size() - 1;
    int mid = 0;
    //中止条件为left<right，则循环结束后left=right
    while (left < right) {
        mid = (left + right) / 2;
        if (nums[mid] > nums[right]) {
            //mid 一定在最小值的左侧
            left = mid + 1;
        } else {
            //注意right与left的处理并不一致。
            //此时的mid可能是最终结果，所以不能直接用mid-1
            right = mid;
        }
    }
    return nums[left];
}

为什么不与num[left]比较

我将本题的代码修改，发现会碰见代码出现错误的问题。而我做的，只是将比较num[right]元素改为比较num[left]元素
代码如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
int findMin(vector < int > & nums) {
    int left = 0;
    int right = nums.size() - 1;
    int mid = (left + right) / 2;
    while (left < right) {
        mid = (left + right) / 2;
        if (nums[mid] >= nums[left]) {
            left = mid + 1;
        } else {
            right = mid;
        }
    }
    return nums[left];
}

发现代码运行出错，经过分析，虽然nums[left]与nums[right]只差了一个数，但是用同样的思路是完全不同的结果

令人迷惑的表象

我需要对官方题解做下补充：
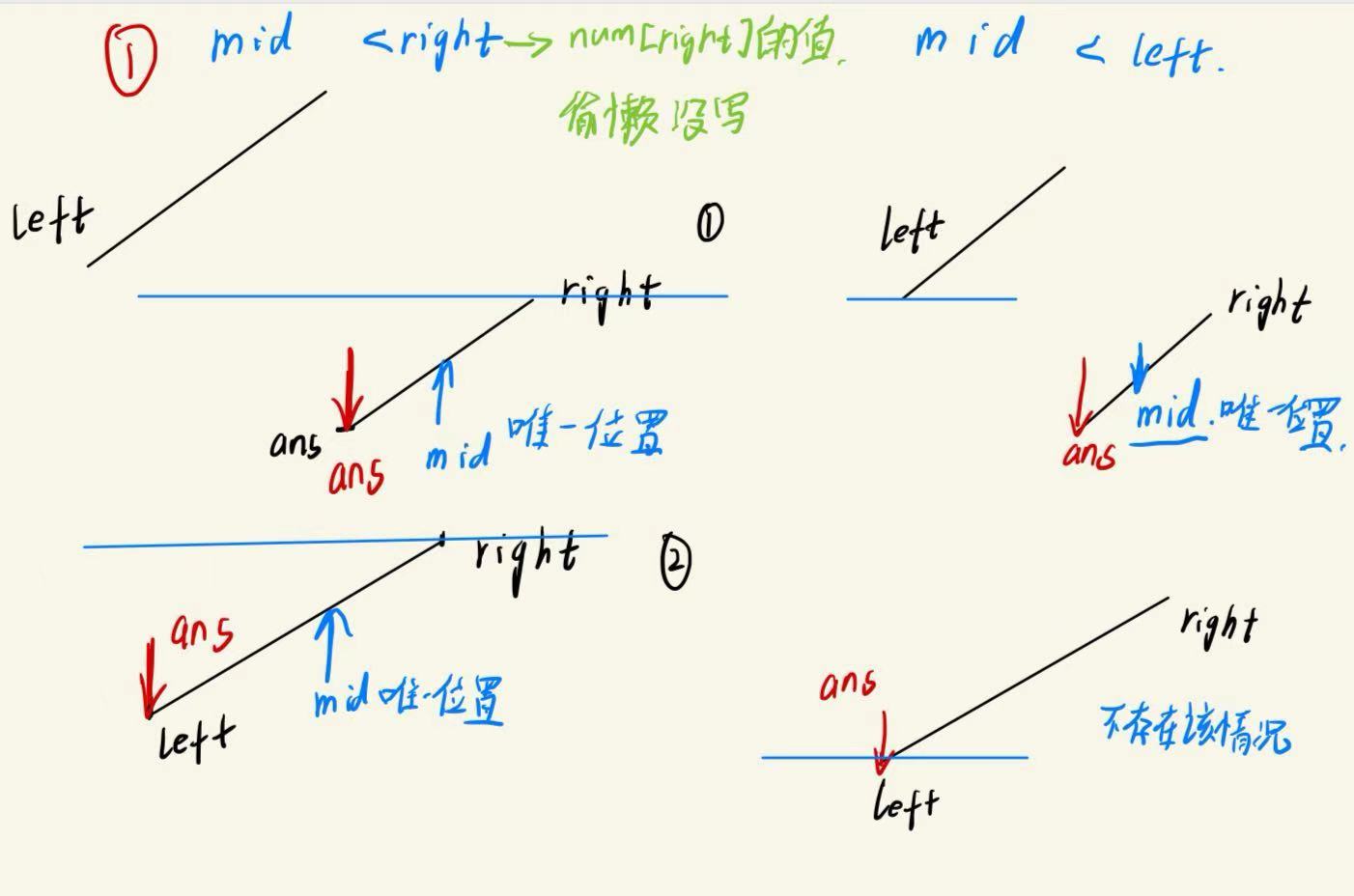
实际上，数组的初始状态有两种：

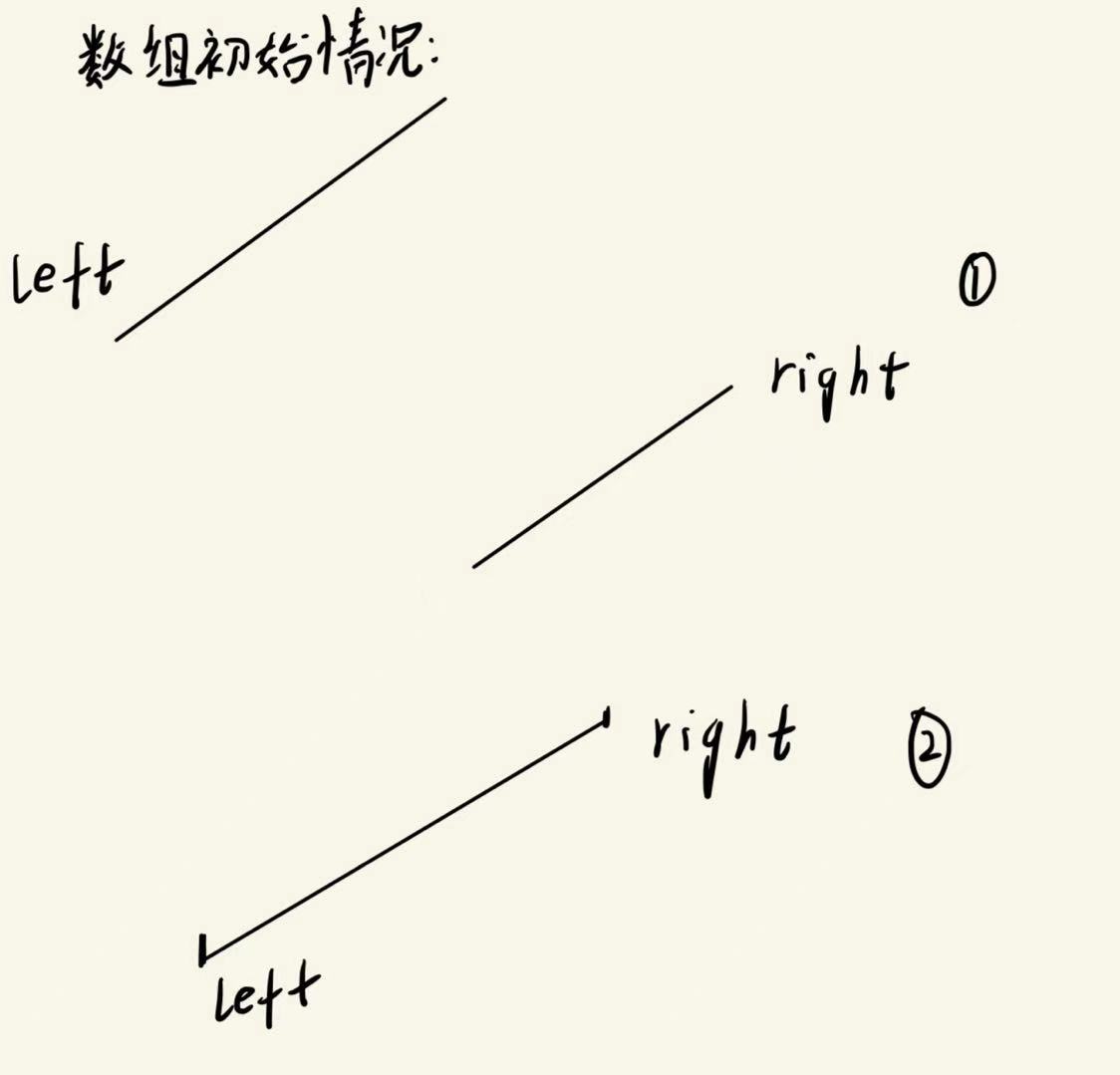
但题解对三种情况的处理是没有问题的(pivot对应mid，high对应right，low对应left)（懒得重画图了）:

  • nums[mid]<nums[right]与nums[mid]<nums[left]
  • nums[mid]==nums[right]与nums[mid]==nums[left]
  • nums[mid]>nums[right]与nums[mid]>nums[left] 与nums[left]进行比较似乎与nums[right]一致，三种情况，可以各自确定mid目前和ans的相对前后关系

为什么会出错？

着重观察
nums[mid]>nums[left]
会发现，在不同的情况下，mid相对于ans的位置前后关系不同，并且情况一在一次次递归后可能变为情况2，如图所示：

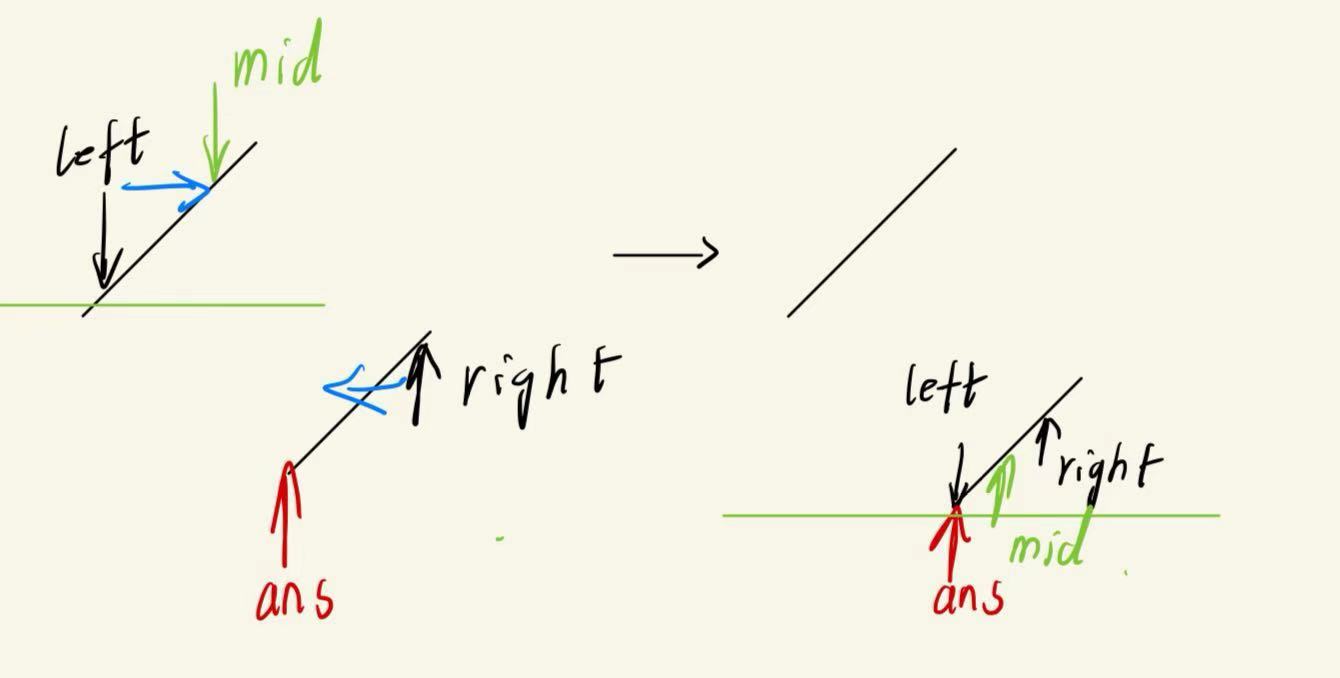
与nums[left]进行比较要处理这种mid与ans前后关系发生变化，逻辑处理不如直接与nums[right]进行比较来的方便。

发散思维

在分析出错原因时，我们指出left，ans，mid，right的相对关系会发生变化，那么存不存在一种可能，使出现下图的变化？：

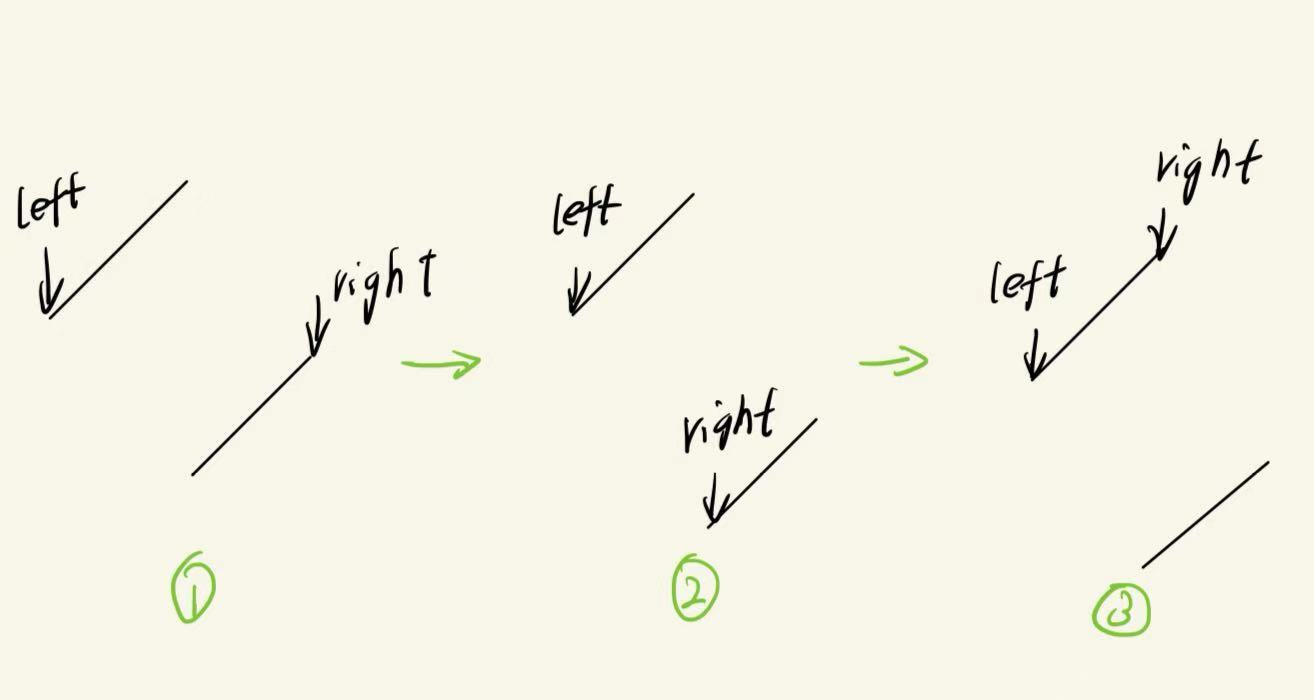
结论：不可能
以下是分析：
分析需要借助代码来分析，

1
2
3
4
5
if (nums[mid] > nums[right]) {
    left = mid + 1;
} else {
    right = mid;
}

变更right条件的是nums[mid]<=nums[right],之前分析可知，由于数组中没有重复的元素，所以在left==right（即循环结束）前，mid一直是不会与right相等的，所以只有nums[mid]<nums[right]时，right才会发生变化，而到达情况2便是极限了，因为直接结束nums[mid]<nums[right]的情况都不会再出现了

寻找最大值怎么办（还有坑）？

按照相同的思路分析问题

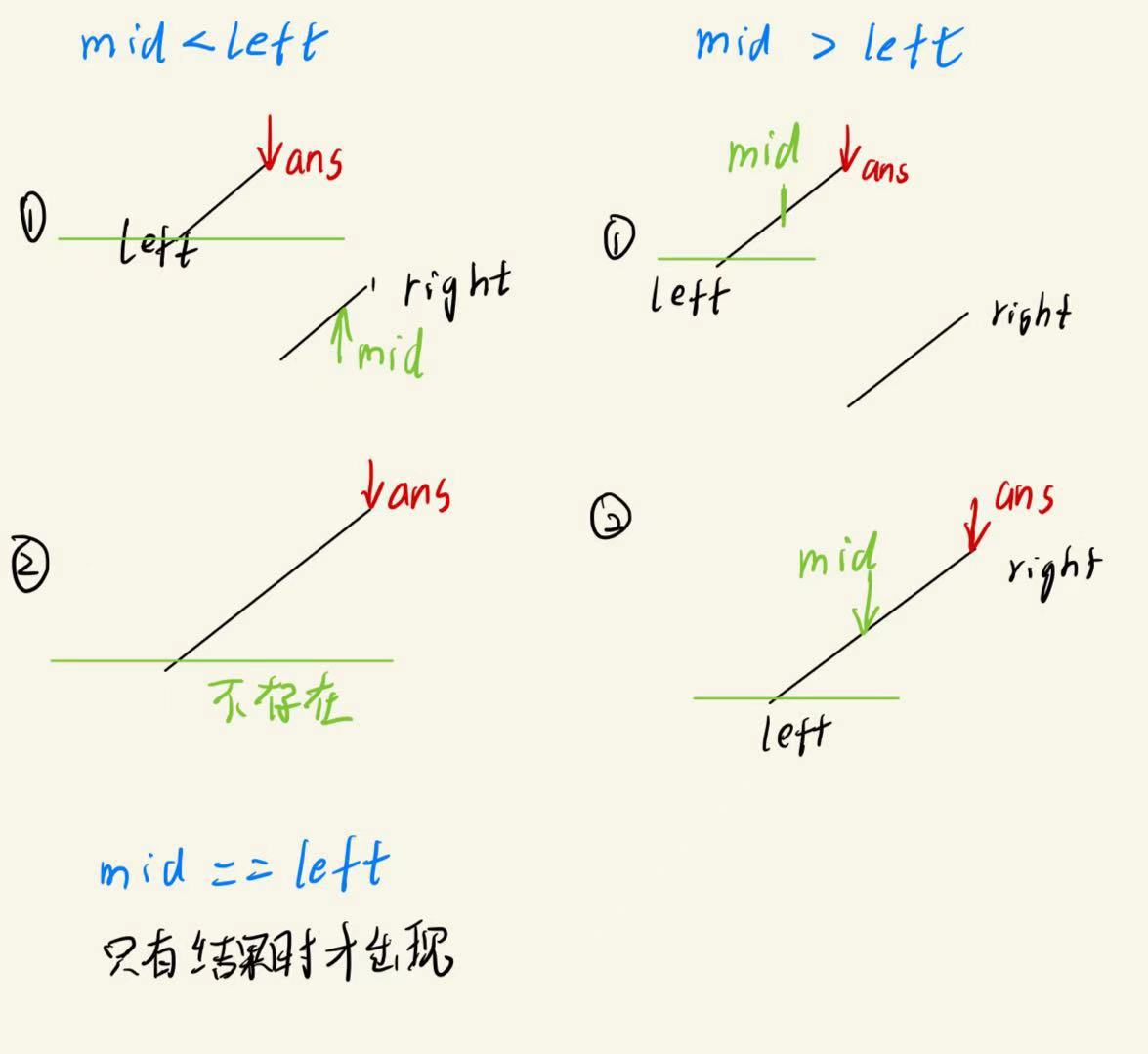
与nums[left]比较

三种情况下，ans与mid的相对情况只有一种

与nums[right]比较

我们发现在nums[mid]<nums[right]时，ans与mid有两种相对位置

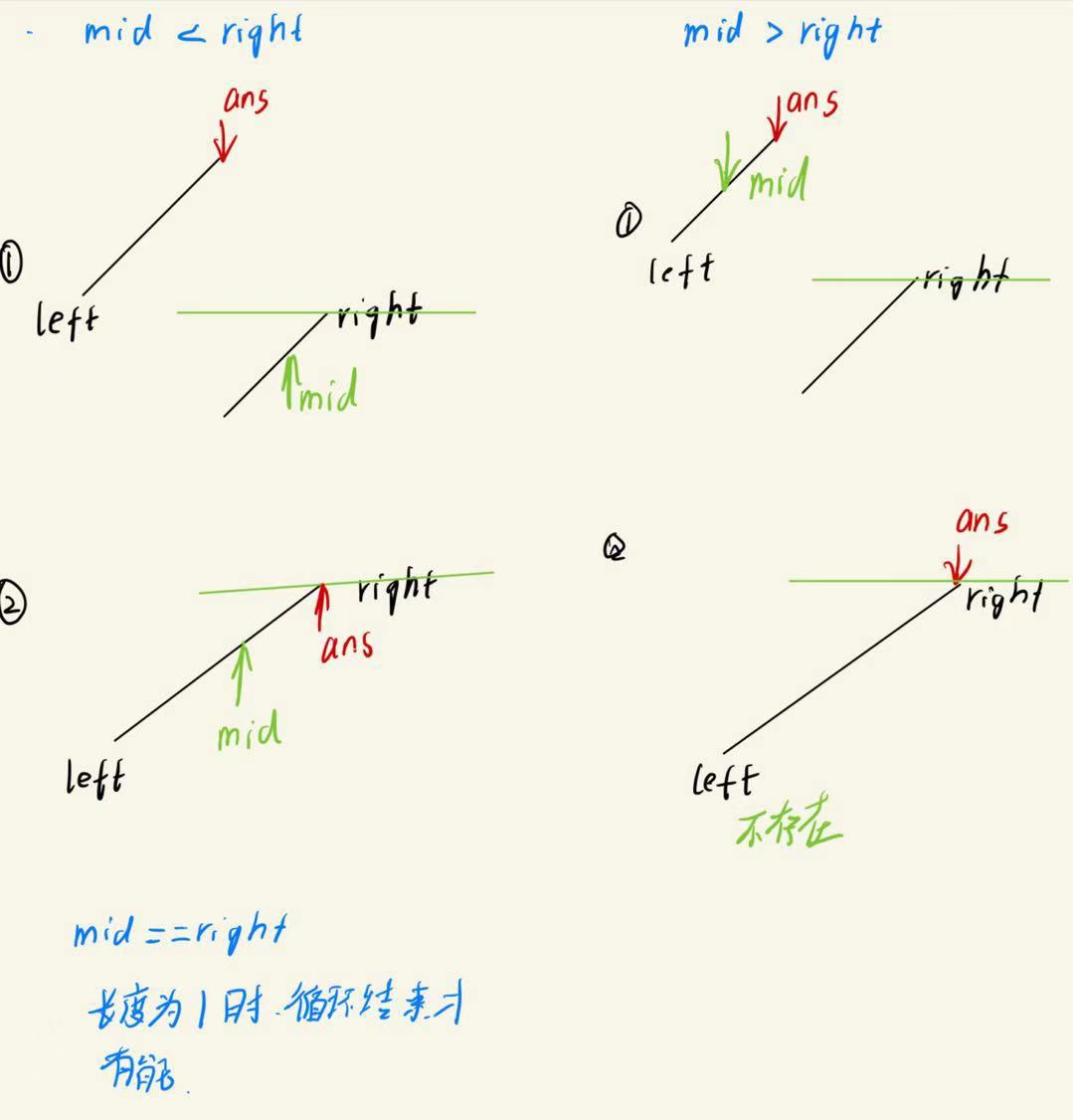
理所应该，以下情况是可能出现的

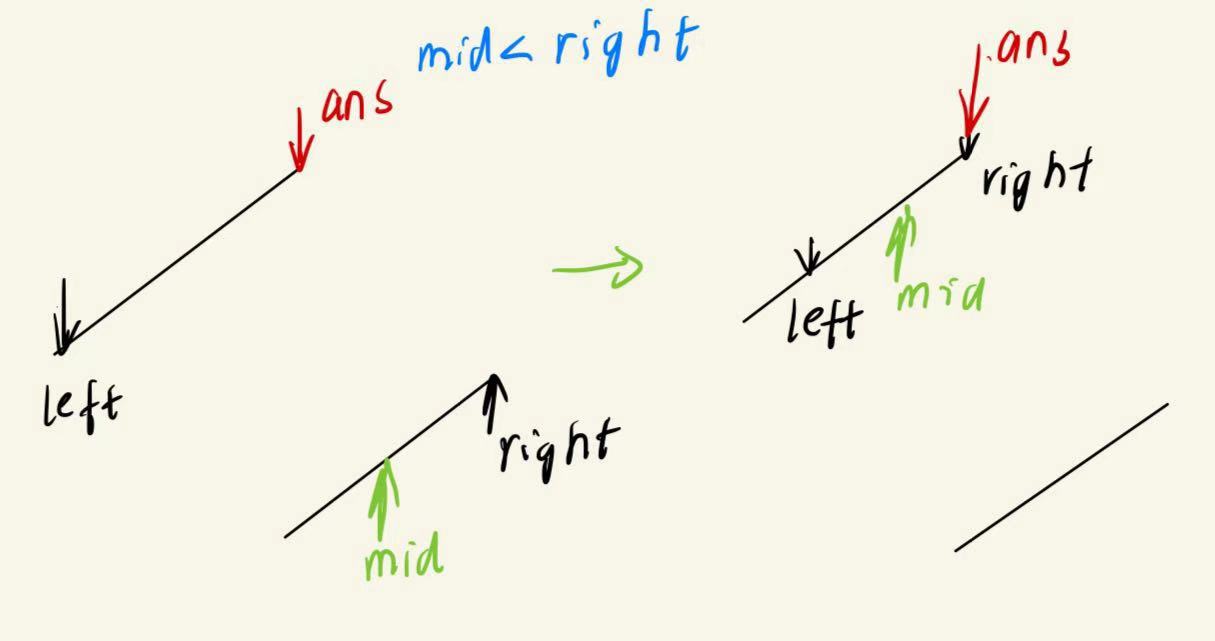
所以，找最小值时为什么不用left和找最大值为什么不用right的原因是相同的：可能一种情况需要处理两套相对关系

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
int findpeek(vector < int > & nums) {
    int l = 0;
    int r = nums.size() - 1;
    while (l < r) {
        int mid = (l + r) / 2;
        if (nums[mid] < nums[l]) {
            r = mid - 1;
        } else {
            l = mid;
        }
    }
    return nums[l];
}

似乎我们使用num[left]就完事大吉了，但实际应用不是这样的。

测试结果

测试发现大部分代码可以通过，但是存在一个测试案例超时

奇怪的是,使用findMin代码寻找最小值，却可以得出正确的结果

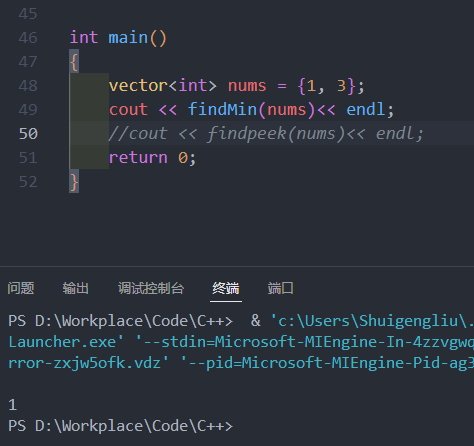
经过分析，我们发现，
mid=(left+right)/2的公式mid边界情况有些特殊，不能想当然。二者之和不为偶数，那么mid值会偏左，导致：

  • 只有数组长度不为1时，mid==right不可能
  • 但是数组长度不为1时,mid==left是可能的。 长度还有可能为2 mid=(left+right)/2=left+(right-left)/2,如果长度大于2，mid也一定不等于left

解决方法

一、将寻找最小值的结果修改一下

既然寻找最大值的坑这么多，我们可以先寻找一个最小值：

  • 若最小值下标为0，最大值即为最后一个元素，
  • 若最小值下标i不为0，最大值即为nums[i-1]
    1
    2
    3
    4
    5
    6
    7
    8
    void findpeek(vector < int > nums) {
        int i = findmin(nums);
        if (i == 0) {
            return nums.size() - 1;
        } else {
            return i - 1;
        }
    }

二、增加数组长度不为1时，mid==left的判断

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
int findpeek(vector < int > & nums) {
    int l = 0;
    int r = nums.size() - 1;
    while (l < r) {
        int mid = (l + r) / 2;
        if (nums[mid] < nums[l]) {
            r = mid - 1;
        } else if (nums[mid] == nums[l]) {
			//l==r时，循环终止，所以此时数组长度一定大于1
			//由于此时长度最大为2，所以长度只能为2
			return nums[l]>nums[r]?nums[l]:nums[r];
        } else {
            l = mid;
        }
    }
    return nums[l];
}